4. 寻找两个正序数组的中位数

Gnomeshgh · 发表于 3 天前

马上注册，结交更多好友，享用更多功能^_^

您需要登录才可以下载或查看，没有账号？立即注册

x

本帖最后由 Gnomeshgh 于 2025-8-21 15:57 编辑

一、题目描述

二、解题思路

（一）暴力解

很明显，两个列表都有序，最简单的思路就是合成一个列表然后取中位数。
直接用列表加法进行合并，然后再对合并后的列表进行排序。最后取中位数。

class Solution:
def findMedianSortedArrays(self, nums1: List[int], nums2: List[int]) -> float:
merged = nums1 + nums2
# 排序
merged.sort()
length = len(merged)
mid = length // 2 # 利用整数除法直接获取中间索引
if length % 2 == 1:
return float(merged[mid])
else:
return (merged[mid - 1] + merged[mid]) / 2.0

复制代码

进行优化，上面的思路需要合并，但是两个列表长度已知，也就是其实可以计算出中位数在第几个，只需要移动到中位数既可。
可以用两个指针指向两个列表，然后谁小谁移动，保存没有移动的数据，直到移动到中位数。
对于偶数而言还需要保存它的左边的数据，也就是在移动前先保存。

class Solution:
def findMedianSortedArrays(self, nums1: List[int], nums2: List[int]) -> float:
# 计算两个数组的长度
nums1_len , nums2_len = len(nums1) , len(nums2)
# 计算两个数组的总长度
total = nums1_len + nums2_len
# 初始化两个数组的指针，分别指向起始位置（0索引）
nums1_p = nums2_p = 0
# 用于存储中位数相关的两个元素：
# right存储当前遍历到的元素，left存储上一次遍历到的元素
right = left = 0
# 遍历到中位数位置：总长度//2 + 1次
# 例如总长度5，需要遍历3次（0,1,2位置）；总长度4，需要遍历3次（0,1,2位置）
for _ in range(total // 2 + 1):
# 将当前right的值保存到left（为偶数长度时计算两个中间值的平均做准备）
left = right
# 指针移动逻辑：
# 1. 确保nums1指针未越界
# 2. 两种情况需要移动nums1指针：
# a. nums2指针已越界（nums2遍历完毕）
# b. nums1当前元素小于nums2当前元素（取较小值推进）
if nums1_p < nums1_len and (nums2_p >= nums2_len or nums1[nums1_p] < nums2[nums2_p]):
# 更新right为nums1当前元素
right = nums1[nums1_p]
# 移动nums1指针到下一位
nums1_p = nums1_p + 1
else:
# 否则移动nums2指针（nums2未遍历完且当前元素更小）
right = nums2[nums2_p]
# 移动nums2指针到下一位
nums2_p = nums2_p + 1
# 根据总长度奇偶性返回结果：
# - 偶数：返回中间两个元素的平均值（left和right）
# - 奇数：返回中间元素（right，因为遍历到了中间位置）
return (left + right) / 2.0 if total % 2 == 0 else float(right)

复制代码

（二）二分法

一般对于有序数组而言会优先想到二分法。
题目求中位数，也就是划分了左右两部分，当是偶数时，左右两部分相等，奇数时，这里让左半部分多1.
也就是在两个数组中找到分割的位置，
假设nums1的分割点为i，（左边有i个，右边有m-i个）
nums2的分割点为j，（左边有j个，右边有n-j个）
当奇数时，即左边最大值就是中间值，此时左半部分是比右半部分多1的
假设总长度为5，则左半部分为3，右半部分为2，此时（m+n+1）// 2 = 3
当为偶数时，左边最大与右边最小之和的二分之一就是中值。
假设总长度为4，则左半部分右半部分都为2，此时（m+n+1）// 2 = 2
所以左半部分总长度的公式为（m+n+1）// 2

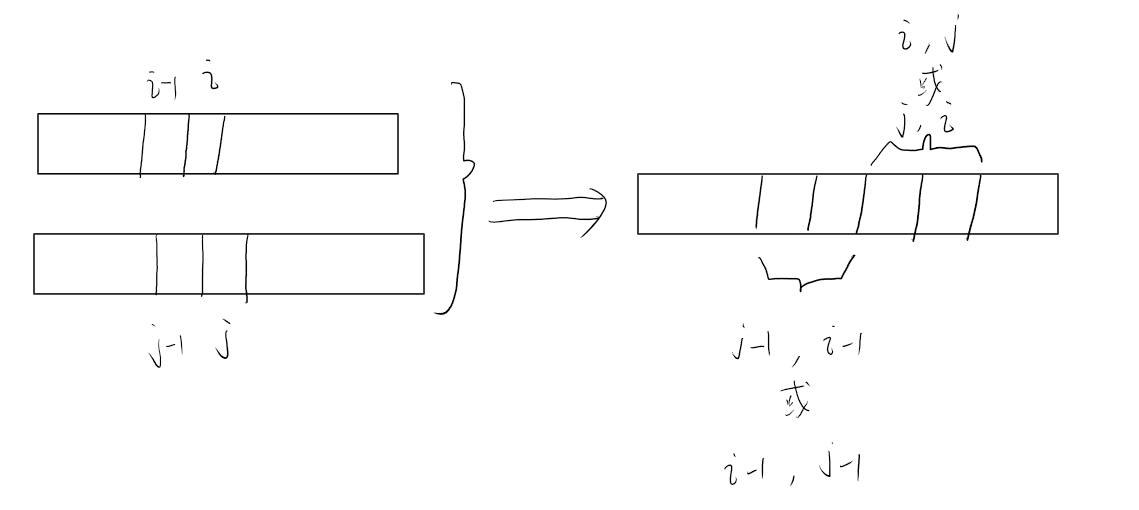
因为前半部分是[0,i-1]和[0,j-1]所以，nums1[i-1]<nums2[j]，nums2[j-1] < nums1
由于已知i就能求出j，所以只需要调整一个就能实现调整两个，
当nums2[j-1] > nums1不符合时，也就是左半部分不全小于右半部分，也就是i要增大，也就是left变大，又因为left是闭合的，所以left = i + 1
其它情况就是right变小，又因为right是开区间，所以right = i
然后不断的向中值逼近，直到退出循环找到最佳的中值位置

class Solution:

def findMedianSortedArrays(self, nums1: List[int], nums2: List[int]) -> float:

      # 1. 确保在较短的数组上进行二分查找，减少二分次数，优化时间复杂度

      # 因为二分查找的时间复杂度取决于数组长度，短数组的log值更小

      if len(nums1) > len(nums2):

         nums1, nums2 = nums2, nums1



      # 2. 定义基本变量

      m, n = len(nums1), len(nums2)  # m为较短数组长度，n为较长数组长度

      left, right = 0, m  # 二分查找的边界：nums1的分割点i的可能范围（0~m）

      # 左半部分总长度：确保左半元素数量 ≥ 右半（奇数时多1，偶数时相等）

      total_left_length = (m + n + 1) // 2  # 公式统一奇数和偶数情况

      # 3. 二分查找寻找最优分割点i

      # 目标：找到i使得nums1和nums2的左半部分所有元素 ≤ 右半部分所有元素

      while left < right:

         # 计算当前分割点i（向下取整，配合后续逻辑避免死循环）

         i = (left + right) // 2

         # 计算nums2的分割点j：左半总长度固定，j由i决定

         j = total_left_length - i

         # 判断当前i是否需要右移：

         # nums1[i]是nums1右半的最小值，nums2[j-1]是nums2左半的最大值

         # 若nums1右半最小值 < nums2左半最大值，说明i太小（nums1左半需包含更多元素）

         if nums1[i] < nums2[j - 1]:

            left = i + 1  # 右移i，同时保证范围缩小（避免死循环）

         else:

            # 否则i可能过大，左移分割点

            right = i



      # 4. 确定最终分割点i和j

      i , j = left , total_left_length - left

      # 5. 计算左半部分的最大值（中位数的左边界）

      # 处理边界情况：某一数组的左半部分为空

      if i == 0:

         # nums1左半为空，左半最大值只能来自nums2的左半

         max_left = nums2[j - 1]

      elif j == 0:

         # nums2左半为空，左半最大值只能来自nums1的左半

         max_left = nums1[i - 1]

      else:

         # 正常情况：取两个数组左半部分的最大值

         max_left = max(nums1[i - 1], nums2[j - 1])



      # 6. 若总长度为奇数，中位数就是左半部分的最大值（左半比右半多1个元素）

      if (m + n ) % 2 == 1:

         return float(max_left)



      # 7. 若总长度为偶数，还需计算右半部分的最小值（中位数的右边界）

      # 处理边界情况：某一数组的右半部分为空

      if i == m:

         # nums1右半为空，右半最小值只能来自nums2的右半

         min_right = nums2[j]

      elif j == n:

         # nums2右半为空，右半最小值只能来自nums1的右半

         min_right = nums1[i]

      else:

         # 正常情况：取两个数组右半部分的最小值

         min_right = min(nums1[i], nums2[j])

      # 8. 偶数长度时，中位数是左半最大值和右半最小值的平均值

      return (max_left + min_right) / 2

复制代码

FishC · 发表于 3 天前

为了找到两个正序数组的中位数并要求时间复杂度为 O(log(m+n))，我们可以使用二分查找的方法。核心思想是将两个数组分割成左右两部分，使得左半部分的所有元素都小于或等于右半部分的所有元素，然后根据总长度的奇偶性计算中位数。

### 方法思路
1. **确保 nums1 是较短的数组**：这样二分查找的范围更小，效率更高。
2. **计算总长度 total**：total = m + n。
3. **确定左半部分的大小**：left_size = (total + 1) // 2（向上取整）。
4. **在 nums1 上使用二分查找**：找到分割点 i，使得 nums1 的左半部分和 nums2 的左半部分合并后，左半部分的最大值小于等于右半部分的最小值。
5. **调整分割点**：通过比较 nums1[i-1] 和 nums2[j] 以及 nums2[j-1] 和 nums1[i] 来调整 i。
6. **计算中位数**：根据总长度的奇偶性，取左半部分的最大值和右半部分的最小值（或平均值）。

### 解决代码

def findMedianSortedArrays(nums1, nums2):
# 确保 nums1 是较短的数组
if len(nums1) > len(nums2):
nums1, nums2 = nums2, nums1
m, n = len(nums1), len(nums2)
total = m + n
left_size = (total + 1) // 2 # 左半部分的大小（向上取整）
# 在 nums1 上使用二分查找
low, high = 0, m
while low <= high:
i = (low + high) // 2 # nums1 的分割点
j = left_size - i # nums2 的分割点
# 处理边界情况
nums1_left_max = float('-inf') if i == 0 else nums1[i-1]
nums1_right_min = float('inf') if i == m else nums1[i]
nums2_left_max = float('-inf') if j == 0 else nums2[j-1]
nums2_right_min = float('inf') if j == n else nums2[j]
# 检查分割是否正确
if nums1_left_max <= nums2_right_min and nums2_left_max <= nums1_right_min:
# 分割正确，计算中位数
if total % 2 == 1:
return max(nums1_left_max, nums2_left_max)
else:
return (max(nums1_left_max, nums2_left_max) + min(nums1_right_min, nums2_right_min)) / 2.0
elif nums1_left_max > nums2_right_min:
high = i - 1 # i 太大，减小 i
else:
low = i + 1 # i 太小，增大 i
return 0.0 # 不会执行到这里，但为了语法完整

复制代码

### 代码解释
- **确保 nums1 较短**：交换数组以使二分查找更高效。
- **计算 left_size**：左半部分的大小为总长度加一后除以二（向上取整）。
- **二分查找分割点 i**：在 nums1 上调整 i，使得左半部分的最大值小于等于右半部分的最小值。
- **处理边界**：当 i 或 j 为 0 或数组长度时，使用无穷大或负无穷大避免索引错误。
- **计算中位数**：根据总长度奇偶性，返回左半部分最大值或左右部分最大最小值的平均值。

这种方法确保了时间复杂度为 O(log(min(m, n)))，符合要求。

以上回复来自 FishC AI 小助理，如未能正确解答您的问题，请继续追问。

不二如是 · 发表于 3 天前

小甲鱼的二师兄 · 发表于 3 天前

可以哇，学习了

gpa5031 · 发表于前天 08:39

看不懂

Gnomeshgh · 发表于前天 19:26

gpa5031 发表于 2025-8-22 08:39
看不懂

哪里看不懂，你说说，我在改一改

账号		自动登录	找回密码
密码			立即注册

[技术交流] 4. 寻找两个正序数组的中位数

马上注册，结交更多好友，享用更多功能^_^

评分

本帖被以下淘专辑推荐:

相关帖子

浏览过的版块